|
Автор: © Aib
"Кривые, кривые, кривые... Это, конечно, хорошо, но как насчёт чего-го
конкретного? К примеру, как нарисовать самую элементарную окружность?"
Вопрос действительно хороший. Если каждый раз рисовать окружность вручную,
задавая поэтапно якорные и контрольные точки curveTo() (а для хорошей точности
нужно от 6 до 18 кривых!), то очень скоро можно прийти к выводу, что делается
это как-то по другому. И первое, что приходит на ум, написать метод, который бы
рисовал окружность по заданному радиусу и координатам центра, говоря другими
словами, создать прототип (это математический термин, не надо его путать с
понятием прототипа объекта в ООП!).
В двух словах о создании прототипа.
Вообще говоря, можно выделить две группы. Представители первой не зависят от
параметров. Вызывая метод рисования, Мы всегда получаем один и тот же объект в
одном и том же месте клипа. Затем все преобразования делаются по средствам
перемещения, маштабирования и поворота клипа, который содержит этот объект. Это
может быть полезно, к примеру, при создании кнопок, чекбоксов и т.п. Для
создания такого прототипа достаточно просто скопировать код рисования
понравившегося объекта в метод, добавив перед вызовами методов lineTo(),
curveTo() и т.д. ключевое слово this. Всё просто. Вторая группа поинтереснее. В
неё входят прототипы объектов, которым необходимо передавать параметры. К
примеру, спираль имеет определённое количество витков, дуга - определённый угол,
прямоугольник - радиус закригления углов, звезда - количество лучей и т.д. Если
Вам нужна спираль, которая используется несколько раз с различным количеством
витков, то бессмысленно создавать отдельные прототипы для каждой спирали, и
эффективнее создать прототип, отвечающий всему классу данных спиралей (данных,
потому что спирали бывают разные по способу задания и, соответственно, по
внешнему виду). Но в подобных случаях простым копированием блока программного
кода не обойтись. Потребуется придумать некий алгоритм рисования. При создании
алгоритма очень полезной может оказаться математическая формула объекта, если
таковая существует. Иногда проще бывает создать прототипы отдельных частей, а
затем соединить их вместе.
Есть ещё одна деталь. Иногда (на практике -
довольно часто) бывает нужно передавать в качестве параметров угол наклона или
маштаб. Это нужно тогда, когда необходимо, чтобы внутри одного клипа было
нарисовано несколько объктов разного размера и под разным углом.
Но слова
это только слова, поэтому далее Я хотел бы проэллюстрировать всё вышесказанное
на конкретном примере.
Метод рисования эллипса ellipseTo().
Итак,
окружность или дуга, а лучше эллипс, и хорошо бы, чтоб его можно было его
рисовать под углом к осям координат. Немного о самом алгоритме. Если бы у Вас
была нарисована окружность, то чтобы получить эллипс Вы бы растянули клип, в
котором находится окружность, чтобы повернуть его изменили свойство _rotation,
чтобы подвинуть задали новые координаты клипа. Если мы поместим внутрь клипа с
координатами (0;0) вместе с окружностью необходимые для её построения
контрольные(control) и якорные(anchor) точки, затем растянем этот клип, повернём
и переместим, чтобы получить искомый объект, глобальные координаты контрольных и
якорных точек и будут искомыми (т.е., если рисовать по точкам с этими
координатами кривую, то мы опять же получим искомый объект). Именно таким
образом мы будем находить координаты контрольной или якорной точки: сначала для
окружности, потом, после растяжения, для эллипса, потом для повёрнутого эллипса,
и, наконец, для перемещённого. Теперь, после определения алгоритма осталось
самая малость - написать программный код. Ну как, приступаем?
Для начала
опишем метод:
movieClip.prototype.ellipseTo = function(){
var t =
arguments[0][0] == undefined ? 1 : 0;
var CenterX =
arguments[0+t][0];
var CenterY = arguments[0+t][1];
var Dir =
1;
var ARadius;
var BRadius;
var StartAngle = 0;
var
EndAngle = 0;
var ARadAngle = 0;
Кому-то это может показаться
непонятным: почему в круглых скобках после имени метода ничего нет, откуда
взялся массив arguments, да ещё и двумерный, и как при таком описании этот метод
вызывать??? Сейчас всё разъясню.
Наш метод - это достаточно мощный
инструмент. Как уже было выше сказано, с его помощью можно будет рисовать эллипс
(или его часть) под заданным углом к осям координат. А для этого нам нужно
передать функции координаты центра, длины радиусов эллипса, начальную и конечную
точки дуги (в данном примере эти параметры задаются углами между прямой,
проходящей через начало (конец) дуги и центр эллипса, и горизонтальной осью
координат) и угол между главной осью эллипса и горизонтальной осью координат.
Кроме того, в некоторых случаях бывает нужно не перемещать начальную точку для
рисования дуги с помощью moveTo(), а начать рисовать с того места, где
закончилась предыдущая линия. Стало быть нужен флаг. Всего восемь параметров.
Но, допустим, нам нужна просто окружность, для которой достаточно трёх
параметров (координаты центра и радиус). И что тогда делать с остальными
параметрами? Поэтому было бы хорошо сделать наш метод таким, чтобы он мог
работать с разным количеством параметров.
Наш метод будет иметь 8
аргументов: Dir(флаг, показывающий, используется ли moveTo() в начале рисования
и в каком направлении нужно рисовать эллипс) [CenterX, CenterY] (координаты
центра), [ARadius, BRadius] (радиусы эллипса), [StartAngle, EndAngle] (начало и
конец дуги в градусах) и ARadAngle (угол между главной осью эллипса, длина
которой задаётся параметром ARadius, и горизонтальной осью координат). Именно в
таком порадке. Из них параметры Dir, [StartAngle, EndAngle] и ARadAngle могут
быть не заданы, кроме того, если нужна окружность, вместо массива параметров
[ARadius, BRadius] можно передать один параметр Radius. К примеру, следующий
набор аргументов
(1, [100, 200], 50, [45, 270])
будет означать,
что нужно нарисовать дугу от 45 до 270 градусов, с центром в точке (100, 200) и
радиусом 50, moveTo() не требуется и строить её нужно в направлении отсчёта
углов. А этот набор
([200, 150], [100, 80], 70)
будет означать,
что нужен эллипс с радиусами (100, 80), с центром в точке (200, 150) и
наклонённый под углом 70 градусов.
Теперь о массиве arguments. Этот
массив создаётся автоматически для каждого метода и содержит все его аргументы.
Двумерным он получился потому, что некоторые из передаваемых аргументов в свою
очередь являются массивами (к примеру, [CenterX, CenterY]). Я использовал массив
arguments, а не описал все эти аргументы в круглых скобках, потому что в
программе будет происходить изменение переменных StartAngle и EndAngle, и если
бы мы описали их в круглых скобках (..., [StartAngle, EndAngle],...), то
изменения отразились бы и на передаваемом массиве. Если же отказаться от
использования массива, то нельзя будет сделать автоопределение того, хотим ли мы
целую фигуру или только дугу. Кроме того, в любом случае потребуется переход из
градусной меры в радианную.
Переменная t принимает значение 1, если был
задан флаг Dir и 0, если нет. Если НЕ был, то считается, что moveTo()
используется. Эта переменная также показывает, с какого места в массиве
arguments следуют все остальные данные. К примеру, если флаг не задан, то массив
[CenterX, CenterY] находится в ячейке arguments[0], а если задан - то
arguments[1]. Поэтому мы просто прибавляем переменную к номеру ячейки (в этом же
примере arguments[0+t]).
И ещё немного о смысле флага Dir и его
применении в нашем методе. Зачем он вообще нужен? Дело в том, что если при
использовании заливки применить метод moveTo(), то предыдущая линия
автоматически замыкается. Этот эффект не всегда желателен, и в этих случаях
moveTo() не используется (как правило, оно и не нужно, так как при обресовке
границы заливки дуга начинается там, где закончилась предыдущая линия). С другой
стороны, когда заливка не используется, и нужно просто нарисовать пару отдельных
окружностей, нет никакой необходимости вручную указывать место начала рисования
линии. Теперь о значениях, которые в данном примере может принимать флаг. В
процессе рисования границы заливки может также оказаться важным, в каком
направлении происходит рисование дуги. На практике это проявляется в том, какой
конец дуги должен примыкать к уже имеющейся части контура. Поэтому Я решил
использовать флаг и для определения направления: значение 1 по направлению
отсчёта углов, -1 - против. Значение по умолчанию равно 1, т.е. если moveTo()
используется, то рисуем в направлении отсчёта углов.
Итак, мы определили
все параметры. Но значения присвоили только пяти, да и то три из них обнулили.
Дело в том, что координаты центра [CenterX, CenterY] существуют независимо от
того, что мы хотим получить: окружность, эллипс или дугу. Параметрам StartAngle,
EndAngle и ARadAngle присваиваются значения "по умолчанию". Почему
именно такие, будет видно далее.
В процессе вычислений нам потребуются
ещё две переменные, которым при описании также задаём некоторые значения по
умолчанию:
var div = 12;
var delta = Math.PI/6;
Далее в
программе будет много операций с использованием методов класса Math. Чтобы
каждый раз при их вызове не писать конструкцию типа Math.method(), воспользуемся
функцией with():
with
(Math){
...............
............... //программный код
...............
}
Функция with здесь действует
совершенно также, как и с клипами. Если вызывается метод или переменная без
указания родителя, то Flash сначала просматривает все методы и переменные,
описанные внутри блока, а затем, если не находит, ищет их в указанном классе (в
данном случае Math).
ВАЖНО!!! Использование with облегчает написание
кода, но сильно замедляет выполнение программы компьютером. В статье Я
использовал with для облегчения восприятия и повышения читабельности кода. Если
для Вас высокая скорость не является важной, то можете использовать with, но для
повышения производительности лучше пару минут понажимать Ctrl+v и установить
везде прямые ссылки. В исходнике, прилагающемся к статье, метод описан без
использования with.
Начнём определять значение остальных параметров.
Итак, сначала выясним, в каком направлении нужно рисовать, если направление было
задано:
if (t == 1 && (arguments[0] == -1 || arguments[0] ==
1)){
Dir = arguments[0];
}
Напомню, что если при вызове
метода мы задаём флаг Dir, то считается, что начальная точка дуги задаётся
концом предыдущей линии и использовать moveTo() для её получения не нужно. Здесь
же проверяем, правильно ли задан флаг.
Теперь определим, что мы рисуем -
эллипс или окружность:
if (arguments[1+t][0] ==
undefined){
ARadius = BRadius = arguments[1+t];
} else
{
ARadius = arguments[1+t][0];
BRadius =
arguments[1+t][1];
};
Проверяем, является ли второй аргумент
массивом. Если нет, то значение первого элемента массива, которого нет,
естественно равно undefined, задан один радиус и тогда оба радиуса эллипса
принимают одно значение. Если да, то переменной ARadius присваиваем значение
первого элемента массива, BRadius - значение второго.
Теперь разберёмся с
параметрами StartAngle, EndAngle и ARadAngle:
with (Math){
if (arguments.length > 2+t){
if (arguments[2+t][0]
== undefined){
ARadAngle =
PI*arguments[2+t]/180;
} else {
StartAngle =
PI*arguments[2+t][0]/180;
EndAngle =
PI*arguments[2+t][1]/180;
Первая строчка проверяет, заданы ли ещё
какие-нибудь аргументы, кроме первых двух/трёх (массив координат центра и массив
радиусов эллипса/радиус окружности, плю учитываем флаг Dir). Если условие
выполнено, то проверяем, является ли третий аргумент массивом. Если нет, то это
угол между главной осью эллипса и горизонтальной осью координат. Присваиваем его
значение переменной ARadAngle, переведённое из градусной меры в радианную, и
процесс передачи аргументов метода его локальным переменным на этом закончен. А
вот если третий аргумент - массив, то это значения углов начала и конца дуги.
Присваиваем их переменным StartAngle и EndAngle (снова предварительно переводя
их из градусной меры в радианную) и затем...
Затем следует фрагмент
кода, в котором происходит преобразование значений углов начала и конца дуги.
if (ARadius != BRadius){
if
(cos(StartAngle) < 0){
StartAngle =
PI+atan(ARadius*tan(StartAngle)/BRadius);
} else if
(cos(StartAngle) > 0){
StartAngle =
atan(ARadius*tan(StartAngle)/BRadius);
};
if
(cos(EndAngle) < 0){
EndAngle =
PI+atan(ARadius*tan(EndAngle)/BRadius);
} else if
(cos(EndAngle) > 0) {
EndAngle =
atan(ARadius*tan(EndAngle)/BRadius);
};
};
Вспомним,
как устроем наш алгоритм: сначала строим окружность (здесь и далее, когда в
тексте будут упоминаться окружность, дуга или эллипс и преобразования, связанные
с ними, подразумевается, что речь идёт о контрольных и якорных точках), затем
растягиваем окружность по горизонтали до эллипса, поворачиваем эллипс на
заданный угол и в конце переносим его из начала координат в заданную точку
(CenterX, CenterY). На стадии маштабирования значения углов меняются. Поэтому мы
сразу меняем значения начального и конечного углов дуги, чтобы после
маштабирования получить исходный угол. Преобразования имеет смысл делать только
в том случае, если у нас эллипс, поэтому проверяется неравенство
радиусов.
Эти преобразования - вопрос чисто математический, поэтому если
вы имеете представление об аффинных преобразованиях или просто не хотите вникать
в суть процесса, можете пропустить следующий абзац. Всех остальных прошу
взглянуть на рисунок:
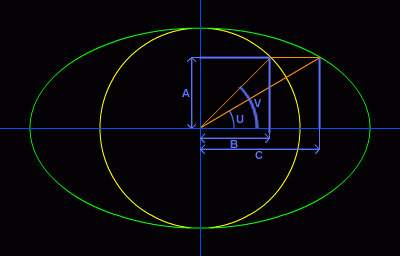
Итак, пусть задан угол U.
Если произвести обратное преобразование эллипса в окружность, то получится
некоторый угол V. Значит, если в начале задать вместо угла U угол V, то после
растягивания мы снова получим угол U. Вычислим угол V. tan(V) = A/B; tan(U) =
A/C; C = B*k, где k - коэффициэнт растяжения, равный отношению горизонтального
радиуса к вертикальному (k = ARadius/BRadius). Отсюда tan(V) = tan(U)*C/B =
tan(U)*B*k/B = tan(U)*k. Именно из этого соотношения берётся формула StartAngle
= atan(ARadius*tan(StartAngle)/BRadius) для начального угла и аналогичная для
конечного. Теперь о проверках, связанных со знаком cos. tan(PI/2) и tan (3*PI/2)
не существуют (равны бесконечности), cos(PI/2)=cos(3*PI/2)=0. Однако, если угол
U=PI/2 или 3*PI/2, при растяжении окружности вдоль горизонтальной оси его
значение не изменится. Поэтому случай, когда cos(StartAngle) = 0 мы сразу
убираем. Проверка формальна, так как скорее всего, если попросить Flash вывести
значение tan(PI/2), вы получите что-то вроде 1.63317787283838e+16, большое, но
всё же конечное число. Если cos(StartAngle) < 0, то
PI/2<StartAngle<3*PI/2, а значение atan(...) всегда лежит между -PI/2 и
PI/2. В этом случае к ответу мы прибавляем PI радиан.
Ну, со сложными
математическими преобразованиями пока всё. Возвращаемся к программному
коду:
while (!(EndAngle >
StartAngle)){
StartAngle -=
2*PI;
};
while (EndAngle-StartAngle >
2*PI){
EndAngle -= 2*PI;
};
Дуга строится всегда от начального угла к конечному, поэтому если
значение начального угла не меньше конечного, то мы уменьшаем StartAngle на 2*PI
радиан за шаг, пока оно не станет меньше EndAngle (забудем пока о том, что
построение может идти и в противоположном напрпвлении - от большего угла к
меньшему). Второй цикл следит за тем, чтобы разница между углами не была больше
2*PI радиан.
Теперь вспомним про описанные вначале переменные div и
delta:
div =
ceil(6*(EndAngle-StartAngle)/PI);
delta =
(EndAngle-StartAngle)/div;
Переменная div показывает, какое количество
дуг нам нужно взять при условии, что каждая из них не больше PI/6 радиан (в
случае, когда углы не заданы как аргументы метода, div = (2*PI-0)/(PI/6) = 12,
что является её значением по умолчанию). А переменная delta - сколько радиан
точно составляет каждая дуга (по умолчанию delta = (PI*2-0)/12 = PI/6). Как Я
уже говорил в первой части статьи, из параболы эллипс можно получить только с
определённой долей приближения. Чем больше кривых curveTo() мы используем, тем
более точное получаем приближение. Если для создания дуги в PI/6 радиан будет
использована одна curveTo(), то точность приближения будет 927/1000, что Я
считаю вполне достаточным. Если вам этого мало (много), просто разделите в
строке div = ceil(6*(EndAngle-StartAngle)/PI) выражение (EndAngle-StartAngle) на
меньший (больший) угол, а также измените значения по умолчанию div и delta.
Скажу лишь, что если на PI/36 радиан отводить одну кривую curveTo(), то точность
будет составлять 9997/10000. Так что брать ещё меньший угол вряд ли имеет
смысл.
И в завершении передачи аргументов для случая рисования
дуги:
if (arguments.length ==
4){
ARadAngle =
PI*arguments[3+t]/180;
};
};
};
Проверка,
задан ли четвёртый аргумент - угол наклона. И закрывающие фигурные
скобки.
Итак, на данный момент код программы выглядит
так:
movieClip.prototype.ellipseTo = function(){
var t =
arguments[0][0] == undefined ? 1 : 0;
var CenterX =
arguments[0+t][0];
var CenterY = arguments[0+t][1];
var Dir =
1;
var ARadius;
var BRadius;
var StartAngle = 0;
var
EndAngle = 0;
var ARadAngle = 0;
var div = 12;
var delta =
Math.PI/6;
if (t == 1 && (arguments[0] == -1 || arguments[0] ==
1)){
Dir = arguments[0];
}
if (arguments[1+t][0] ==
undefined){
ARadius = BRadius = arguments[1+t];
} else
{
ARadius = arguments[1+t][0];
BRadius =
arguments[1+t][1];
};
with (Math){
if
(arguments.length > 2+t){
if (arguments[2+t][0] ==
undefined){
ARadAngle =
PI*arguments[2+t]/180;
} else {
StartAngle =
PI*arguments[2+t][0]/180;
EndAngle =
PI*arguments[2+t][1]/180;
if (ARadius !=
BRadius){
if (cos(StartAngle)<
0){
StartAngle =
PI+atan(ARadius*tan(StartAngle)/BRadius);
} else if
(cos(StartAngle)> 0){
StartAngle =
atan(ARadius*tan(StartAngle)/BRadius);
};
if
(cos(EndAngle)< 0){
EndAngle =
PI+atan(ARadius*tan(EndAngle)/BRadius);
} else if
(cos(EndAngle)> 0) {
EndAngle =
atan(ARadius*tan(EndAngle)/BRadius);
};
};
while
(!(EndAngle > StartAngle)){
StartAngle -=
2*PI;
};
while (EndAngle-StartAngle >
2*PI){
EndAngle -= 2*PI;
};
div =
ceil(6*(EndAngle-StartAngle)/PI);
delta =
(EndAngle-StartAngle)/div;
if (arguments.length ==
4){
ARadAngle =
PI*arguments[3+t]/180;
};
};
};
Подготовка данных окончена. Приступаем к нахождению координат
контрольных и якорных точек. Нам потребуются ещё две константы, радиусы эллипса,
которому принадлежат все контрольные точки, участвующие в
построении:
var ABRadius = ARadius/cos(delta/2);
var
BBRadius = BRadius/cos(delta/2);
Чтобы понять, почему все они лежат на
одном эллипсе, опять придётся ненадолго углубится в математику (желающие могут
снова пропустить пару абзацев). Вспомним, как создаётся наш эллипс: сначала
находим координаты контрольных и якорных точек для окружности, затем растягиваем
по X, затем поворачиваем и в конце переносим. Итак, пусть у нас есть часть
окружности:
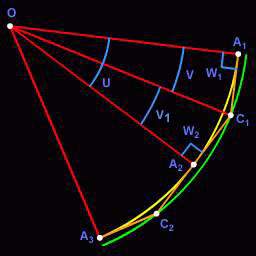
Угол U - это наша delta. После
задания параметров методу выяснилось, что для построение дуги потребуется две
curveTo(). В общем случае их может быть от одной до двенадцати (полная
окружность или эллипс), но на данном этапе нам потребуется всего одна, так что
их общее количество пока не важно. Для начала найдём угол V. Отрезки A2_C1 и
A1_C1 являются направляющими векторами для curveTo, поэтому они являются
касательными, в данном случае к заданной окружности. А значит они
перпендекулярны радиусам O_A2 и O_A1 соответственно по свойству касательных к
окружности. Значит, треугольники O_A2_C1 и O_A1_C1 прямоугольные. Они имеют одну
общую сторону O_C1, а стороны O_A2 и O_A1 равны как радиусы окружности. Значит,
эти треугольники равны, и угол V = V1. В сумме они дают угол U, а значит угол V
= U-V1 = U-V = U/2. Теперь найдём O_C1. По определению cos(V) = A1_C1/O_C1.
Отсюда O_C1 = A1_C1/cos(U/2). Отсюда получается формула BBRadius =
BRadius/cos(delta/2). Как видно, при постоянных BRadius и delta, BBRadius также
будет постоянен. BBRadius - расстояние от центра окружности до любой участвующей
в построении контрольной точки. Значит, все контрольные точки равноудалены от
центра заданной окружности, т.е. сами лежат на окружности с тем же центром и
радиусом BBRadius. Теперь, если мы рассмотрим соседнюю дугу, то для неё
направляющий вектор curveTo A2_C2 также будет перпендекулярен O_A2. Тем самым
выполняется условие отсутствия изломов: контрольная и якорная точки первой
кривой и контрольная точка второй кривой находятся на одной
прямой.
Теперь переходим к эллипсу. Если вспомнить нашу ассоциацию
растяжением клипа, содержащего окружность, то естественно, вместе с нарисованной
окружностью растягивается и воображаемая, на которой находятся контрольные
точки.
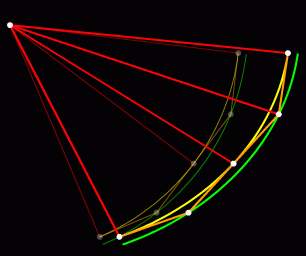
Поэтому после растяжения они также будут
находится на некотором эллипсе. Его горизонтальный радиус ABRadius = BBRadius*k
= (BRadius/cos(delta/2))*(ARadius/BRadius) = ARadius/cos(delta/2), так как
коэффициэнт растяжения у них одинаковый. Так как при растяжении прямые остаются
прямыми (меняются лишь углы между ними), то условие отсутствия изломов
по-прежнему сохраняется.
Итак, начинаем нахождение координат точек! Чтобы
не делать два цикла и не заводить новые массивы с данными, мы будем находить
координаты контрольной и якорной точек и сразу вызывать curveTo(). Но сначала,
если флаг Dir не был задан, нужно найти координаты стартовой точки, к которой мы
перейдём через moveTo():
if (t==0){
var teX =
ARadius*cos(StartAngle);
var teY =
BRadius*sin(StartAngle);
var X1 =
CenterX+teX*cos(ARadAngle)-teY*sin(ARadAngle);
var Y1 =
CenterY+teX*sin(ARadAngle)+teY*cos(ARadAngle);
this.moveTo (X1,
Y1);
}
Если бы точка лежала на окружности с центром в начале
координат, то её координаты были бы (BRadius*cos(StartAngle),
BRadius*sin(StartAngle)). Так как в общем случае мы производим растяжение, то
координату X нужно домножить на ARadius/BRadius. Итак, переменные teX и teY
содержат координаты стартовой точки на неповёрнутом эллипсе с центром в начале
координат.
Теперь нужно выполнить поворот. Для этого используется
формула:
// X' = X*cos(u)-Y*sin(u)
// Y' =
X*sin(u)+Y*cos(u)
где X, Y - старые координаты точки, X', Y' - новые, u -
угол поворота. Желающие могут посмотреть коротенький вывод этих формул:
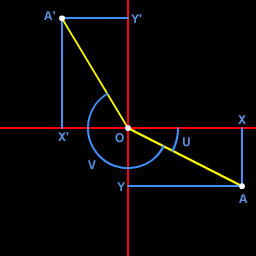
Итак, координаты точки А (X, Y). Пусть длина отрезка О_А
равна L. Тогда X=L*cos(u); Y=L*sin(u). Теперь производим поворот на угол V.
Точка A перешла в A' с координатами X'=L*cos(u+v); Y'=L*sin(u+v). Теперь
раскрываем скобки по формулам синуса и косинуса суммы:
X'=L*cos(u+v)=L*cos(u)*cos(v)-L*sin(u)*sin(v)=X*cos(v)-Y*sin(v), аналогично
X'=L*sin(u+v)=L*sin(u)*cos(v)+L*cos(u)*sin(v)=Y*cos(v)+X*sin(v).
Последнее,
что осталось сделать, это переместить точку в соотвествии с заданным центром
эллипса. Для этого просто прибавляем к координатам точки соответствующие
значения координат центра.
Теперь чуть-чуть опртимизируем
код.
if (t==0){
var te =
ARadius*cos(StartAngle);
var Y1 =
BRadius*sin(StartAngle);
var X1 =
CenterX+teX*cos(ARadAngle)-teY*sin(ARadAngle);
Y1 =
CenterY+teX*sin(ARadAngle)+teY*cos(ARadAngle);
this.moveTo (X1,
Y1);
}
В качестве второй временной переменной используем Y1,
значение которой изменяется лишь в конце этой части кода. Ещё одна вещь: если Вы
привыкли, что отсчёт углов происходит против часовой стрелки, а не по часовой,
то нужно как-бы перевернуть ось Y, и пятая строчка тогда будет выглядеть
так:
Y1 = CenterY-te*sin(ARadAngle)-Y1*cos(ARadAngle);
И,
наконец, учитывая, что переменнные X1, Y1 и te потребуются в цикле независемо от
того, используем мы moveTo() или нет, делаем окончательный
вариант:
var X1;
var Y1;
var te;
if (t==0){
te =
ARadius*cos(StartAngle);
Y1 =
BRadius*sin(StartAngle);
X1 =
CenterX+teX*cos(ARadAngle)-teY*sin(ARadAngle);
Y1 =
CenterY+teX*sin(ARadAngle)+teY*cos(ARadAngle);
this.moveTo (X1,
Y1);
}
Теперь, если флаг Dir всё же был задан и равен -1, то
нужно поменять местами значения начального и конечного
углов:
else if (Dir==-1){
te =
StartAngle;
StartAngle = EndAngle;
EndAngle =
te;
}
В цикле потребуются ещё две переменные для хранения
координат контрольных точек. Пока просто опишем их:
var
X2;
var Y2;
Ну, все преготовления закончились. Запускаем цикл
рисования эллипса:
for (var i = 1; i<=div;
i++){
te = ARadius*cos(StartAngle+Dir*delta*i);
Y1
= BRadius*sin(StartAngle+Dir*delta*i);
X1 =
CenterX+te*cos(ARadAngle)-Y1*sin(ARadAngle);
Y1 =
CenterY+te*sin(ARadAngle)+Y1*cos(ARadAngle);
te =
ABRadius*cos(StartAngle+Dir*delta*(i-0.5));
Y2 =
BBRadius*sin(StartAngle+Dir*delta*(i-0.5));
X2 =
CenterX+te*cos(ARadAngle)-Y2*sin(ARadAngle);
Y2 =
CenterY+te*sin(ARadAngle)+Y2*cos(ARadAngle);
this.curveTo (X2,
Y2, X1, Y1);
};
};
}
Цикл пройдёт div раз и создаст
div дуг. Сначала находим координаты для якорных точки. Всё происходит по тому же
принципу, что и для начальной точки . На каждом этапе работы цикла мы смещаемся
на угол delta относительно предыдущего положения, в конце концов достигая
конечного угла EndAngle = StartAngle+Dir*delta*div. Переменная Dir указывает,
нужно прибавлять угол или вычитать, в завсимости от выбранного направления
построения.
Координаты контрольных точек находятся аналогично якорным,
так как тоже находятся на эллипсе. Угол берётся на delta/2 меньше, чем для
якорной точки (это следует из проведённых ранее вычислений). Опять же, если
нужно другое направление отсчёта,
Y1 =
CenterY-te*sin(ARadAngle)-Y1*cos(ARadAngle)
Y2 =
CenterY-te*sin(ARadAngle)-Y2*cos(ARadAngle);
И, наконец, вызов метода
curveTo(), ради которого были все наши труды.
ВСЕ!!! Создание окончено.
Целиком код метода выглядит так:
movieClip.prototype.ellipseTo =
function(){
var t = arguments[0][0] == undefined ? 1 : 0;
var
CenterX = arguments[0+t][0];
var CenterY = arguments[0+t][1];
var
Dir = 1;
var ARadius;
var BRadius;
var StartAngle =
0;
var EndAngle = 0;
var ARadAngle = 0;
var div =
12;
var delta = Math.PI/6;
with (Math){
if
(arguments[1+t][0] == undefined){
ARadius = BRadius =
arguments[1+t];
} else {
ARadius =
arguments[1+t][0];
BRadius =
arguments[1+t][1];
};
if (arguments.length >
2+t){
if (arguments[2+t][0] ==
undefined){
ARadAngle =
PI*arguments[2+t]/180;
} else {
StartAngle =
PI*arguments[2+t][0]/180;
EndAngle =
PI*arguments[2+t][1]/180;
if (ARadius !=
BRadius){
if (cos(StartAngle)<
0){
StartAngle =
PI+atan(ARadius*tan(StartAngle)/BRadius);
} else if
(cos(StartAngle)> 0){
StartAngle =
atan(ARadius*tan(StartAngle)/BRadius);
};
if
(cos(EndAngle)< 0){
EndAngle =
PI+atan(ARadius*tan(EndAngle)/BRadius);
} else if
(cos(EndAngle)> 0) {
EndAngle =
atan(ARadius*tan(EndAngle)/BRadius);
};
};
while
(!(EndAngle > StartAngle)){
StartAngle -=
2*PI;
};
while (EndAngle-StartAngle >
2*PI){
EndAngle -= 2*PI;
};
div =
ceil(6*(EndAngle-StartAngle)/PI);
delta =
(EndAngle-StartAngle)/div;
if (arguments.length ==
4){
ARadAngle =
PI*arguments[3+t]/180;
};
};
};
var
te;
var X1;
var Y1;
var X2;
var
Y2;
if (t==0){
te =
ARadius*cos(StartAngle);
Y1 =
BRadius*sin(StartAngle);
X1 =
CenterX+teX*cos(ARadAngle)-teY*sin(ARadAngle);
Y1 =
CenterY+teX*sin(ARadAngle)+teY*cos(ARadAngle);
this.moveTo (X1,
Y1);
} else if (Dir==-1){
te =
StartAngle;
StartAngle = EndAngle;
EndAngle =
te;
}
for (var i = 1; i<=div; i++){
te =
ARadius*cos(StartAngle+Dir*delta*i);
Y1 =
BRadius*sin(StartAngle+Dir*delta*i);
X1 =
CenterX+te*cos(ARadAngle)-Y1*sin(ARadAngle);
Y1 =
CenterY+te*sin(ARadAngle)+Y1*cos(ARadAngle);
te =
ABRadius*cos(StartAngle+Dir*delta*(i-0.5));
Y2 =
BBRadius*sin(StartAngle+Dir*delta*(i-0.5));
X2 =
CenterX+te*cos(ARadAngle)-Y2*sin(ARadAngle);
Y2 =
CenterY+te*sin(ARadAngle)+Y2*cos(ARadAngle);
this.curveTo (X2,
Y2, X1, Y1);
};
};
}
Впрочем, рекомендую скачать
исходник и посмотреть программный код целиком именно там (во избежании возможных
опечаток 8-)).
Надеюсь, что данная статья была для Вас полезной.
В
завершении хочу выразить благодарность Nox Noctis'у - за предпросмотр и
критику.
До свидания! Удачи!
Литература по FLASH
|